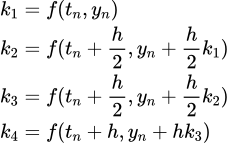引子
在 Filed Play:简介中提到了这个方法,查资料了解了一下。
- Origin
- My GitHub
相关概念
极限
有时不能直接计算某个值,但可以看看逐渐接近时的情况,看下面的例子:
当 x = 1 时,发现结果是 0/0 ,这个在数学上是未定式,是不确定的。那看看接近的情况:
| x | f(x) |
|---|---|
| 0.5 | 1.5 |
| 0.9 | 1.9 |
| 0.99 | 1.99 |
| 0.9999 | 1.9999 |
| 0.999999 | 1.999999 |
发现当 x 接近 1 的时候,f(x) 越来越接近 2 ,这种情况就是极限。
我们可以说当 x 趋近 1 时,f(x) 的极限是 2 ,用符号表示就是:
更加正式的定义见这里。
导数
设函数 f(x) 在 x0 有定义,如果以下极限存在:
则称 f(x) 在 x0 处可导,上述极限值为 f(x) 在 x0 处的导数,记作 f'(x0) 。
导数描述的是函数的变化率,在几何中可以通过导数计算出某一点切线的斜率。
求导法则见这里。
微分
设函数 y=f(x) 在 x0 处连续,若存在实数 A ,使得:
其中 △x -> 0 ,则称 f(x) 在 x0 处可微,线性部分 A△x 为 f(x) 在 x0 处的微分,记作 dy 。
微分的几何意义是线性替代,线性替代的思想可以推广至高阶替代。
更加详细的介绍见这里。
微分方程
微分方程指的是含有函数及其导数的方程。微分方程中有的有无穷多解,有的无解,有的则仅有有限个解。
微分方程的阶数取决于方程中出现的最高次导数阶数。
- 常微分方程:仅含有一个独立变量的微分方程。
- 偏微分方程:函数包含两个或两个以上的独立变量。
- 特解:满足微分方程的某一个解。
- 通解:满足微分方程的一组解。
- 初值问题:满足初值条件的常微分方程的解。
- 单步法:计算下一个点的值 yn+1 只需要用到前面一个点的值 yn 。
- 多步法:计算下一个点的值 yn+1 需要用到前面 m 个点的值 ym 。
更多信息见这里和这里。
Runge-Kutta
龙格-库塔法是一种求解常微分方程数值解的单步算法。其中有一个在工程上应用很广泛,称为 RK4 。
对于一阶微分方程初值问题:
其中,t0 为初始时间(已知常数),y0为初始状态(已知向量),f(t,y) 是关于时间 t 和状态 y 的函数(已知函数)。
RK4 求解算法为:
其中:
h 为时间步长。
参考资料
- Runge–Kutta methods wiki
- Runge–Kutta methods mathworld
- Runge-Kutta方法及其推导
- 龙格库塔法